Triangle Puzzle

( If you can't explain this enigma, you can always cut out the pieces and baffle the grandkids! )

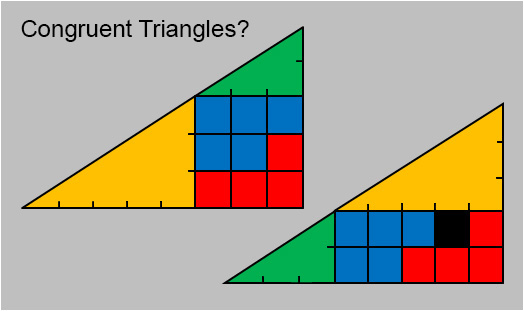
Where did that Black Square come from?

First: a confession!  I've distorted the two large triangles ever so slightly so visitors with a good grasp of school mathematics won't immediately spot the explanation for this seemingly impossible situation.  When the Blue, Green, Red and Yellow pieces are arranged in the top formation, they fit neatly together to form an '8 x 5' right-angled triangle.  When they are rearranged into the bottom formation, the resulting triangle miraculously contains an extra square.  Surely this can't be possible.  As Bobby Thompson might have concluded,"There's a rabbit off!"

You may remember from your schooldays that the area of a triangle can easily be calculated by multiplying its base by its height and then dividing that answer by 2.  Let's assume that each square making up these two triangles measures 1 inch x 1 inch.  Both triangles have a base of 8 inches and a height of 5 inches, therefore they both have the same area: (8 x 5) / 2 = 20 square inches.  But hang on a minute!  The Blue, Red, Yellow and Green pieces haven't changed in size, so where did that Black Square come from?  That's the problem you have to solve.

If you can remember some basic maths, the explanation should eventually dawn on you.  The clues are staring you in the face.

[ A quotation from Aristotle to get you thinking along the right lines: "The whole is greater than the sum of its parts." ]